This article is about some squashing functions of deep learning, including Softmax Function, Sigmoid Function, and Hyperbolic Functions. All of these three functions are used to squash value to a certain range.
Softmax Function
Softmax Function: A generalization of the logistic function that "squashes" a K-dimensional vector z of arbitrary real values to a K-dimensional vector $$ \sigma ( \mathbf z ) $$ of real values, where each entry is in the range (0, 1], and all the entries add up to 1.
$$ {\displaystyle \sigma : \mathbb{R}^{K}\to \left{ \sigma \in \mathbb{R}^{K} | \sigma_{i} > 0, \sum_{i=1}^{K} \sigma_{i} = 1 \right}} $$
$$ \sigma ( \mathbf{z} )_{j}={ \frac{e^{z_{j}}}{ \sum_{k=1}^{K} e^{z_{k}} } } \quad \text{for j=1, ..., K.} $$
In probability theory, the output of the softmax function can be used to represent a categorical distribution - that is, a probability distribution over K different possible outcomes.
The softmax function is the gradient of the LogSumExp function.
LogSumExp Function
LogSumExp Function: The LogSumExp(LSE) function is a smooth approximation to the maximum function.
$$ LSE(x_1, ..., x_n) = log(\sum_{i=1}^{n} e^{x_i}) $$
($$log$$ stands for the natural logarithm function, i.e. the logarithm to the base e.)
When directly encountered, LSE can be well-approximated by $$ max { x_1, ..., x_n } $$ :
$$ max { x_1, ..., x_n } \leq LSE(x_1, ..., x_n) \leq max { x_1, ..., x_n } + log(n) $$
Sigmoid Function
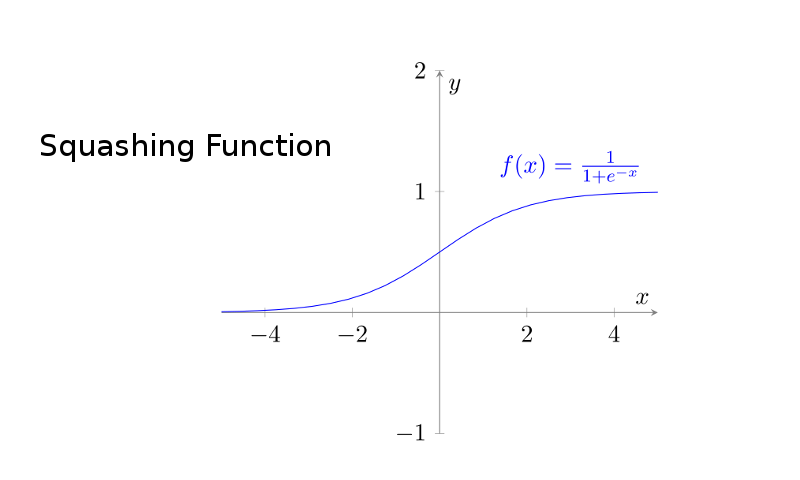
Sigmoid Function: A mathematical function with a "S"-shaped curve.
One frequent used sigmoid function in ML is the logistic function.
Logistic Function:
$$ f(x) = \frac{1}{1+e^{-x}} $$
$$ \tikz \node [scale=1.1] { \begin{tikzpicture}[] \begin{axis}[ axis line style=gray, ymin=-1, ymax=2, axis x line=center, axis y line=center, xlabel=$x$, ylabel=$y$ ] \addplot[blue]{1/(1+exp(-x))}; \addplot[blue] coordinates{(3,1.2)} node{$f(x)=\frac{1}{1+e^{-x}}$}; \end{axis} \end{tikzpicture} }; $$
To understand how it work, first we differentiate it:
$$ f\prime(x) = \frac{1}{2+e^{x}+e^{-x}} $$
$$ \tikz \node [scale=1.1] { \begin{tikzpicture}[] \begin{axis}[ axis line style=gray, ymin=-1, ymax=1, axis x line=center, axis y line=center, xlabel=$x$, ylabel=$y$ ] \addplot[blue]{1/(2+exp(x)+exp(-x))}; \addplot[blue] coordinates{(3,0.3)} node{$f(x)=\frac{1}{2+e^{x}+e^{-x}}$}; \end{axis} \end{tikzpicture} }; $$
Since function $$ g(x) = e^{x}+e^{-x} $$ is a (hyperbolic ?) curve which looks like a quadratic function, it's clear that $$ f\prime(x) $$ will go up to 0.25 from 0, from negative infinity to 0, and than go down to 0 again, from 0 to positive infinity.
So from the derivative, we can see that logistic function will be in "S"-shape, with its value very close to 0 when x getting closer and closer to negative infinity, and with its value very close to 1 when x getting near positive infinity. The turning point of tendency is 0, where the second derivative is 0 and where the value of the logistic function is 0.5.
Hyperbolic Function
Inspired by Euler's formula, $$ e^{i\theta} = cos(\theta) + i sin(\theta) $$, hyperbolic functions extend the notion of the parametric equations for a unit circle to the parametric equations for a hyperbola. ( From Hyperbolic Trigonometric Function | Brilliant Math & Science Wiki )
Notice: Hyperbolic Tangent is also a sigmoid function according to wikipedia Sigmoid Function.
Six hyperbolic functions :
| hyperbolic | connection with trigonometric | |
|---|---|---|
| sine | $$ sinh(x) = \frac{e^x - e^{-x}}{2} $$ | $$ sinh(x)=-i sin(ix) $$ |
| cosine | $$ cosh(x) = \frac{e^x + e^{-x}}{2} $$ | $$ cosh(x) = cos(ix) $$ |
| tangent | $$ tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} = \frac{1-e^{-2x}}{1+e^{-2x}} $$ | $$ tanh(x) = -i tan(ix) $$ |
| cotangent ($$ = \frac{1}{tan(x)} $$) | $$ coth(x) = \frac{e^x + e^{-x}}{e^x - e^{-x}} , \quad {x \ne 0} $$ | $$ coth(x) = i cot(ix) $$ |
| secant ($$ = \frac{1}{cos(x)} $$) | $$ sech(x) = \frac{2}{e^x + e^{-x}} $$ | $$ sech(x) = sec(ix) $$ |
| cosecant ($$ = \frac{1}{sin(x)} $$) | $$ csch(x) = \frac{2}{e^x - e^{-x}} , \quad {x \ne 0} $$ | $$ csc(x) = i csc(ix) $$ |
Graph of these functions :
$$ \tikz \node [scale=1.1] { \begin{tikzpicture}[] \begin{axis}[ samples=120, axis line style=gray, ymin=-5, ymax=5, axis equal, axis x line=center, axis y line=center, xlabel=$x$, ylabel=$y$, ] \addplot[green]{(exp(x)-exp(-x))/2}; \addlegendentry{sinh} \addplot[red]{(exp(x)+exp(-x))/2}; \addlegendentry{cosh} \addplot[blue]{(exp(x)-exp(-x))/(exp(x)+exp(-x))}; \addlegendentry{tanh} \end{axis} \end{tikzpicture} }; $$
$$ \tikz \node [scale=1.1] { \begin{tikzpicture}[] \begin{axis}[ samples=120, axis line style=gray, ymin=-5, ymax=5, axis equal, axis x line=center, axis y line=center, xlabel=$x$, ylabel=$y$, ] \addplot[green, restrict expr to domain={(x<-0.1)+(x>0.1)}{0.1:+inf}]{(exp(x)+exp(-x))/(exp(x)-exp(-x))}; \addlegendentry{coth} \addplot[red]{2/(exp(x)+exp(-x))}; \addlegendentry{sech} \addplot[blue, restrict expr to domain={(x<-0.1)+(x>0.1)}{0.1:+inf}]{2/(exp(x)-exp(-x))}; \addlegendentry{csch} \end{axis} \end{tikzpicture} }; $$