
Python 实现: AdaBoost - Donny-Hikari - Github
Introduction
AdaBoost 是 Adaptive Boosting 的简称。 Boosting 是一种 Ensemble Learning 方法。 其他的 Ensemble Learning 方法还有 Bagging, Stacking 等。 Bagging, Boosting, Stacking 的区别如下:
-
Bagging:
Equal weight voting. Trains each model with a random drawn subset of training set. -
Boosting:
Trains each new model instance to emphasize the training instances that previous models mis-classified. Has better accuracy comparing to bagging, but also tends to overfit. -
Stacking:
Trains a learning algorithm to combine the predictions of several other learning algorithms.
The Formulas
Given a N*M matrix X, and a N vector y, where N is the count of samples, and M is the features of samples. AdaBoost trains T weak classifiers with the following steps:
给定一个N*M的矩阵X(特征),和一个N维向量y(标签),N为样本数,M为特征维度。AdaBoost以一下步骤训练T个弱分类器:
-
Initialize. / 初始化 $$ \begin{align*} & W_{0,j} = 1 / N \\ & i = 0 \end{align*} $$
-
Train i-th weak classifier with training set {X, y} and distribution W_i. / 用样本权重和样本训练第i个弱分类器h_i:
-
Get the predict result \( h_i \) on the weak classifier with input X. / 获得样本加权错误和epsilon $$ \begin{align*} & h_i: X \rightarrow {-1, 1} \\ & \epsilon = Pr_{j ~ W_i} [ h_i(X_j) \neq y_j ] \\ & = \sum_{j=1}^{N} ( W_i * ( h_i(X) \neq y ) )
\end{align*} $$ -
Update alpha and normalized weights. / 更新alpha和归一化样本权重 \( W_i \) $$ \begin{align*} & \alpha_{i} = \frac{1}{2} \ln{ \frac{1 - \epsilon}{\epsilon} } \\ & W_{i+1,j} = \frac{W_{i}}{Z_{i+1}} e^{ - \alpha y_j h_{i,j} } \\ \text{where} \quad & Z_{i+1} = \sum_{j=1}^{N} W_{i+1,j}
\end{align*}
$$
Z is a normalization factor.
-
Repeat steps 2 ~ 4 until i reaches T. / 迭代2~3获得T个弱分类器
-
Output the final hypothesis: / 最终分类结果为: $$ H(X) = sign( \sum_{i=1}^{T} ( \alpha_{i} * h_i(X) ) ) $$
Analyzation of the Formulas
-
权重的调整。
权重的调整实际上是 \( W_{i+1,j} = \frac{ W_{i,j} }{ Z_{i+1} } * ( \frac{1 - \epsilon}{\epsilon} )^{-(y_j == h_{i,j})} \). \( h_{i,j} \) 为第i个弱分类器对第j个样本的分类结果。
暂且假设分类错误率e小于0.5 (大于0.5参见[2]).
当且仅当分类正确时,权重调整为原来的 \( \frac{\epsilon}{1 - \epsilon} \). 则该分数小于1,故权重变小。
当且仅当分类错误时,权重调整为原来的 \( \frac{1 - \epsilon}{\epsilon} \). 则该分数大于1,故权重变大。
-
若单个分类器错误率高于50%,会导致正确分类的样本权重增加。
此时,实际上将发生”逆转“。因为alpha为负值,在最后投票时,该分类器的分类结果将相反。因此正确分类的成为错误分类,错误分类的成为正确分类。故而权重的增加仍加在“错误的“分类上,只是该错误是对全局而言。
能够发生“逆转”的关键是 ln 函数。
-
剩下的问题是alpha系数中为何要加 1/2.
思考无果,跟同学讨论了一下。据说是为了方便某些情况下的处理。从原理入手。查了下维基,Rojas 2009 年的推导。颇为清晰。见[Derivation].
Derivation
前 m 个弱分类器分类结果加权和: $$ C_{m}(X_j) = \sum_{i=1}^{m} ( \alpha_i * h_i(X_j) ) $$
定义总错误 E: $$ E = \sum_{j=1}^{N} ( e^{ -y_j * C_{m}(X_j) } ) $$
令 $$ W_{m,j} = \begin{cases} 1, & m = 1 \\ e^{ -y_j * C_{m-1}(X_j) }, & m > 1 \\ \end{cases} $$
则 $$ \begin{align*} E & = \sum_{j=1}^{N} ( W_{m,j} * e^{ -y_j * \alpha_m * h_m(X_j) } ) \\ & = \sum_{ h_m(X_j) = y_j } ( W_{m,j} * e^{ -\alpha_m } ) + \sum_{ h_m(X_j) \neq y_j } ( W_{m,j} * e^{ \alpha_m } ) \\ & = \sum_{j=1}^{N} ( W_{m,j} * e^{ -\alpha_m } ) + \sum_{ h_m(X_j) \neq y_j } ( W_{m,j} * ( e^{ \alpha_m } - e^{ -\alpha_m } ) ) \end{align*} $$
E 对 \( \alpha_m \) 求导 $$ \frac{d E}{d \alpha_m} = \frac{ d ( \sum_{ h_m(X_j) = y_j } ( W_{m,j} * e^{ -\alpha_m } ) + \sum_{ h_m(X_j) \neq y_j } ( W_{m,j} * e^{ \alpha_m } ) ) }{d \alpha_m} $$
由 \( e^{x} + e^{-x} \) 函数曲线(类似二次函数)可知,其在一阶导数为0处取得最小值。令一阶导数等于0,求得 $$ \alpha_m = \frac{1}{2} ln( \frac{ \sum_{ h_m(X_j) = y_j } W_{m,j} }{ \sum_{ h_m(X_j) \neq y_j } W_{m,j} } ) $$
令 \( \epsilon = \frac{ \sum_{ h_m(X_j) \neq y_j } W_{m,j} }{ \sum_{j=1}^{N} W_{m,j} } \),则 $$ \alpha_m = \frac{1}{2} ln( \frac{1 - \epsilon}{\epsilon} ) $$
通过这样计算得到的 \( \alpha \) 能够使总误差 E 最小。
Test Result
Using a demo from sklearn AdaBoost, I got the following result.
Weak classifiers: 200; Iteration steps in each weak classifier: 200:
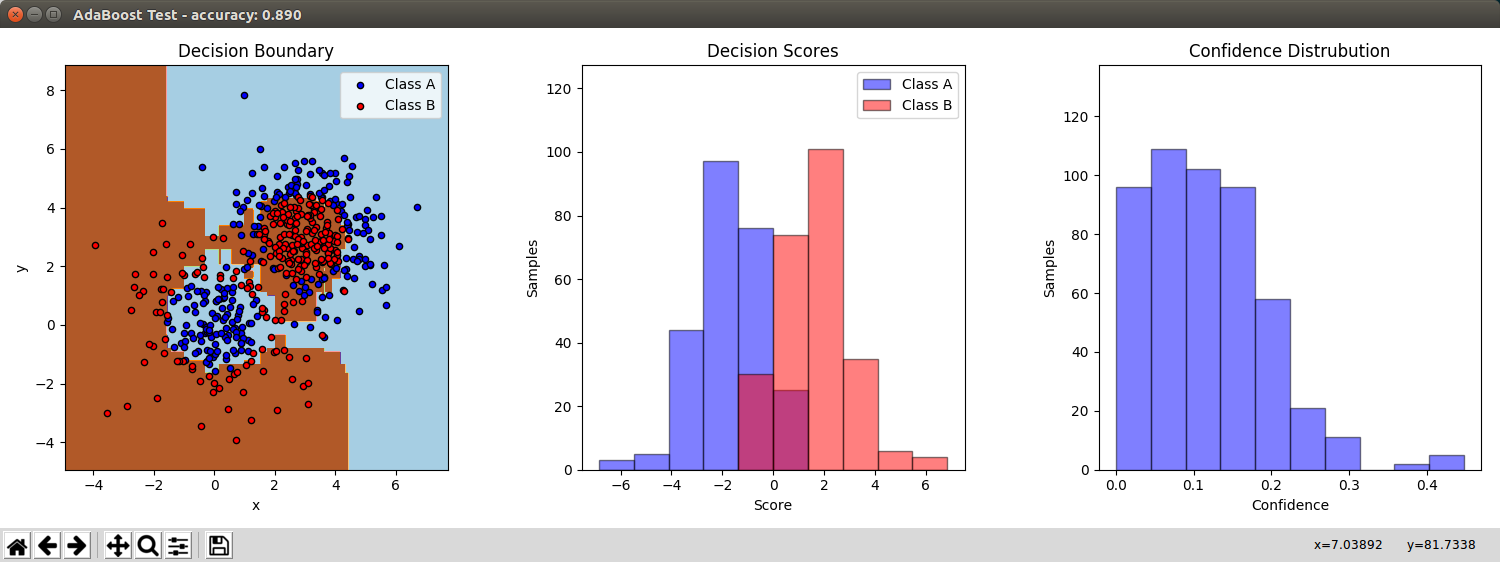
Compares with the AdaBoostClassifier from sklearn with 200 estimators (weak classifiers):
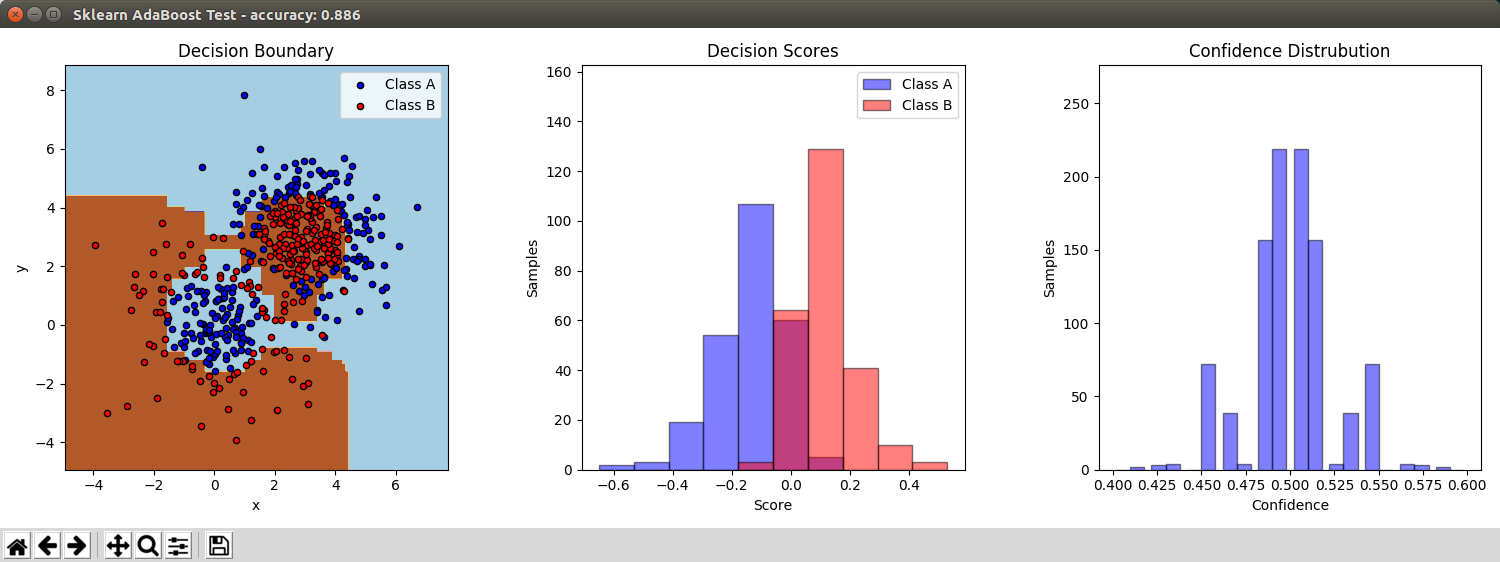
More comparison for my AdaBoostClassifier with different parameters:
| estimators | iteration steps | time | accuracy |
|---|---|---|---|
| 30 | 30 | 0.0621 | 0.8540 |
| 30 | 60 | 0.1095 | 0.8760 |
| 30 | 200 | 0.3725 | 0.8620 |
| 30 | 400 | 0.7168 | 0.8720 |
| 60 | 30 | 0.1291 | 0.8620 |
| 60 | 60 | 0.2328 | 0.8600 |
| 60 | 200 | 0.7886 | 0.8780 |
| 60 | 400 | 1.4679 | 0.8840 |
| 200 | 30 | 0.3942 | 0.8600 |
| 200 | 60 | 0.7560 | 0.8700 |
| 200 | 200 | 2.4925 | 0.8900 |
| 200 | 400 | 4.7178 | 0.9020 |
| 400 | 30 | 0.8758 | 0.8640 |
| 400 | 60 | 1.6578 | 0.8720 |
| 400 | 200 | 5.0294 | 0.9040 |
| 400 | 400 | 10.0294 | 0.9260 |