Review of Linear Algebra

Matrix

Basic Operations

• Matrix Product (Dot Product)
• Matrix Division
• Matrix Multiplication (Hadamard Product)

Matrix Operations

• Matrix Transpose
• Matrix Inversion
• Matrix Trace (the sum of the main diagonal elements)
• Matrix Determinant
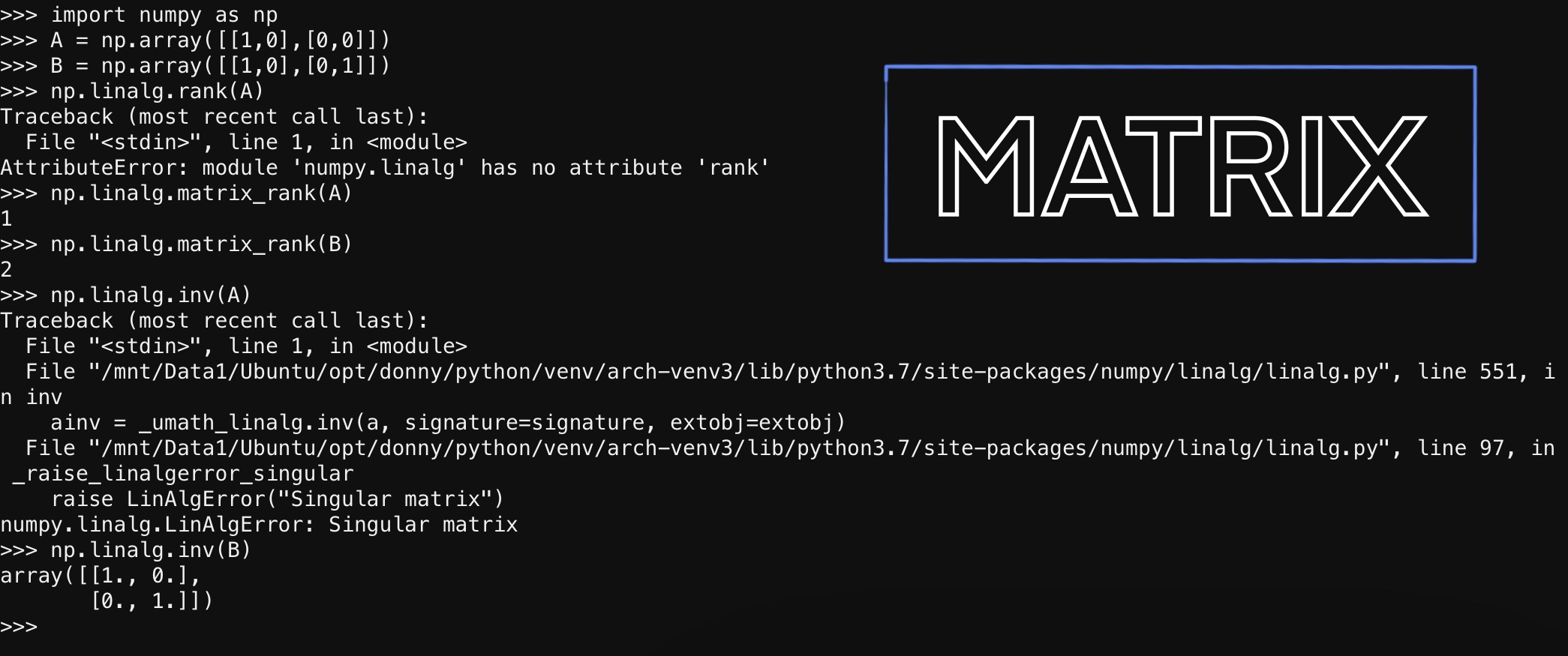
• Matrix Rank (the maximum number of linearly independent columns)

Matrix Factorization (?)

• LU Decomposition
• QR Decomposition
• Eigendecomposition
• Singular Value Decomposition

Ref: Linear Algebra Cheat Sheet Python Code

Others:

• Unitary Matrix
  A matrix \( U \) that satisfies
• Minor Matrix
• Adjugate Matrix
  For square matrix A,  \( adj(A) = C^{T} \) , \( C = (-1)^{i+j} M_{i,j} \) , where \( M_{i,j} \)  is the (i, j) minor of A.
• Conjugate Transpose
  \( (A^{*})_{i,j} = \overline{A_{j,i}} \) , for complex number \( c = a+ib \) , \( \overline{c} = a-ib \)
• Orthogonal Matrix
  A matrix that satisfy \( A^{T} = A^{-1} \)

Matrix Product

Matrix product is produced by taking i-th row of the first matrix and j-th column of the second matrix and calculate dot product of the two vectors as the (i, j) element in the result matrix.

Given

$$ A = \begin{bmatrix} 1 & 2 & 1 \\ 3 & 4 & 2 \ \end{bmatrix} \\ B = \begin{bmatrix} 1 & 2 \\ 2 & 1 \\ 1 & 2 \ \end{bmatrix} \\ $$

then,

$$ AB = \begin{bmatrix} 6 & 6 \\ 13 & 14 \end{bmatrix} $$

Matrix Division

Matrix Division makes use of the following property:

$$ AX = B \\ A^{-1}AX = A^{-1}B \\ X = A^{-1}B $$

where  \( A^{-1} \)  is the inversion of A. Therefore A must be invertible (see Invertible Matrix, in short a matrix is invertible if it has full rank).

See the Matrix Inversion section below for more information.

Matrix Inversion

An n-by-n Matrix A is invertible if there exists an n-by-n matrix B such that \( BA = BA = I_n \) . And B is called the inverse of A.

Only square matrices can be invertible. Non-square matrix may have left-inverse or right-inverse.

A square matrix that is not invertible is called singular or degenerate. A square matrix is singular if and only if its determinant is zero.

Given

$$ A = \begin{bmatrix} 1 & 3 & 3 \\ 1 & 4 & 3 \\ 1 & 3 & 4 \end{bmatrix} $$

The inverse of A, \( A^{-1} \) is calculated by

$$ [A | I ] = \begin{bmatrix} 1 & 3 & 3 & | & 1 & 0 & 0 \\ 1 & 4 & 3 & | & 0 & 1 & 0 \\ 1 & 3 & 4 & | & 0 & 1 & 0 \end{bmatrix} $$

Transform it using Gaussian Elimination (aka. row reduction) so that the left side becomes an identity matrix,

$$ [I | A^{-1}] = \begin{bmatrix} 1 & 0 & 0 & | & 7 & -3 & -3 \\ 0 & 1 & 0 & | & -1 & 1 & 0 \\ 0 & 0 & 1 & | & -1 & 0 & 1 \\ \end{bmatrix} $$

Therefore, \( A^{-1} \) is

$$ A^{-1} = \begin{bmatrix} 7 & -3 & -3 \\ -1 & 1 & 0 \\ -1 & 0 & 1 \\ \end{bmatrix} $$

The inverse can also be calculated as:

$$ A^{-1} = \frac{1}{det(A)} adj(A) $$