Convolutional Neural Network

This article is my reflection on my previous work FaceLock, a project to recognize user's face and lock the computer if the user doesn't present in a certain time. CNN is used to recognize different faces. I watch the Coursera course Convolutional Neural Networks by Andrew Ng to understand more about CNN, so it's also a learning note about it.

One Layer of a Convolutional Network

In a non-convolutional network, we have the following formula:

$$ Z = W \cdot x + b \\ a = g(Z) $$

Similarly, in the convolutional network, we can have:

$$ Z = W * x + b \\ a = g(Z) $$

@ $$*$$ is a convolution operation.

@ $$x$$ is the input matrix.

@ $$W$$ is the filter. Different filter can detect different feature, e.g. vertical edge, diagonal edge, etc.

@ $$b$$ is the bias.

@ $$g$$ is a activation function.

@ $$a$$ is the output matrix, and can be fed to the next layer.

Calculating the Number

The Number of the Parameters

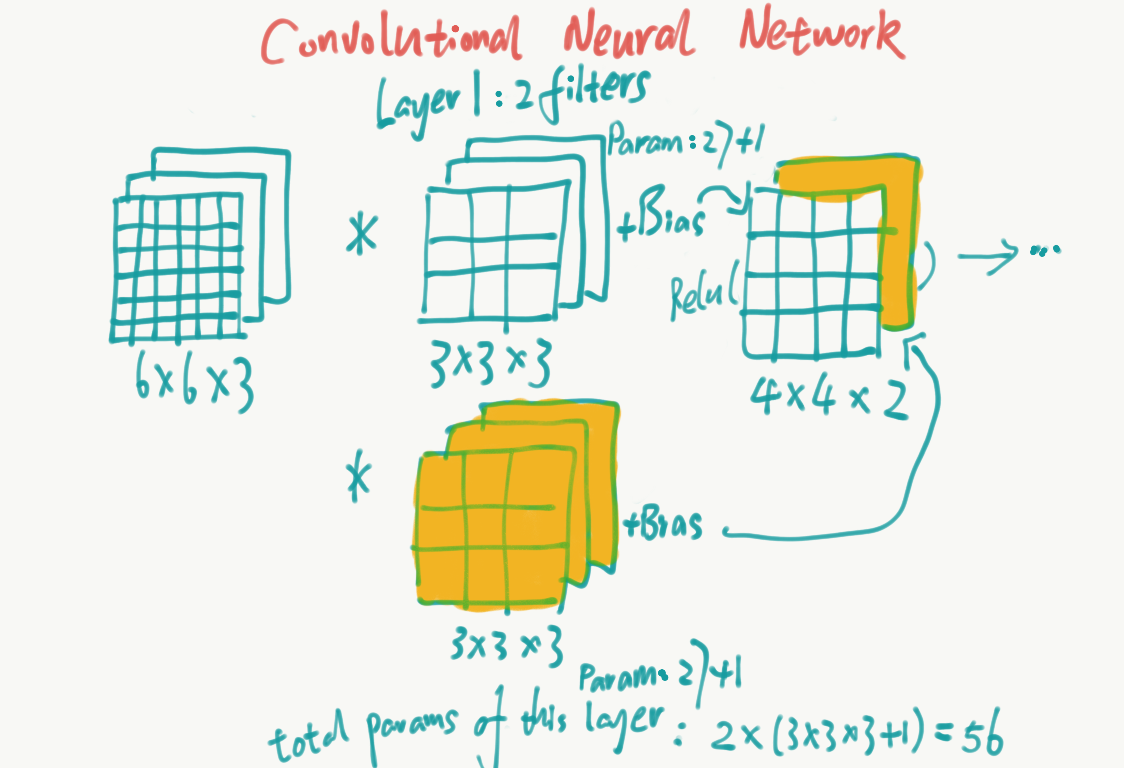
Suppose we have 10 filters which are $$ 3 \times 3 \times 3 $$ in one layer of a neural network, how many parameters does the layer have?

In one filter, there are $$ 3 \times 3 \times 3 + 1 = 28 $$ (1 bias) parameters. So there are $$ 10 \times 28 = 280 $$ parameters in this layer.

The Shape of the Output

Suppose we have a $$ x \times y \times ch $$ (ch is the number of channel) input, $$ n $$ numbers of $$ r \times c \times ch $$ filters, the stride is set to (0, 0), not padding. what will be the output shape?

The output shape will be $$ (x - r + 1) \times (y - c + 1) \times n $$.

Now change the stride to (a, b), what will be the output shape?

The output shape will be $$ (\lfloor \frac{x - r}{a} \rfloor + 1) \times (\lfloor \frac{y - c}{b} \rfloor + 1) \times n $$.

Now add padding $$ (p_x, p_y) $$, what will be the output shape again?

The output shape will be $$ (\lfloor \frac{x + 2 p_x - r}{a} \rfloor + 1) \times (\lfloor \frac{y + 2 p_y - c}{b} \rfloor + 1) \times n $$.

Summary of Notation

Define:

$$ \begin{align*} f^{[l]} & = \text{filter size} \\ p^{[l]} & = \text{padding} \\ s^{[l]} & = \text{stride} \\ n^{[l]}_c & = \text{number of filters} \\ \end{align*} $$

Than we have:

$$ \begin{align*} & \text{Input shape:} & n^{[l-1]}_H \times n^{[l-1]}_W \times n^{[l-1]}_c \\ & \text{Output shape:} & n^{[l]}_H \times n^{[l]}_W \times n^{[l]}_c \\ & \text{s.t.} & n^{[l]}_H = \lfloor \frac{n^{[l-1]}_H + 2 p^{[l]} - f^{[l]}}{s^{[l]}} \rfloor + 1 \\ & \quad & n^{[l]}_W = \lfloor \frac{n^{[l-1]}_W + 2 p^{[l]} - f^{[l]}}{s^{[l]}} \rfloor + 1 \\ & \text{Filter shape:} & f^{[l]} \times f^{[l]} \times n^{[l-1]}_c \\ & \text{Activations:} & a^{[l]} \rightarrow n^{[l]}_H \times n^{[l]}_W \times n^{[l]}_c \\ & \text{Weight:} & f^{[l]} \times f^{[l]} \times n^{[l-1]}_c \times n^{[l]}_c \\ & \text{bias:} & 1 \times 1 \times 1 \times n^{[l]}_c \end{align*} $$

In batch gradient descent, Activation is

$$ A^{[l]} \rightarrow m \times n^{[l]}_H \times n^{[l]}_W \times n^{[l]}_c $$

where $$ A^{[l]} $$ is a set of $$ m $$ activations if there are $$ m $$ examples.